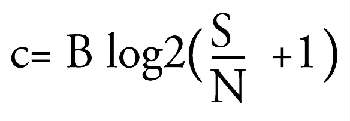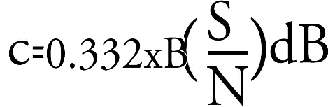.
La
figura qui accanto mostra un riassunto di tutto il procedimento della conversione
di un segnale analogico in un segnale digitale, visto nell'articolo precedente.
Ciascuna immagine può essere infatti considerata come
una serie di variazioni di luce bidimensionali, ovvero, nel senso
della larghezza e dell'altezza.
Provate a mettere gli occhi su un' immagine, ad esempio, su una
qualunque fotografia. Analizzate l'angolo superiore sinistro: ha una determinata
luminosità. Se procediamo all' analisi in una direzione (ad
esempio da sinistra a destra) ecco che si incontra una variazione di luminosità.
In altre parole, se spostiamo l'attenzione verso destra vediamo che
questo valore di luminosità può crescere o diminuire, oppure
crescere ancora, e così via in un saliscendi tra lo scuro e il chiaro.
Quello che è rappresentato in alto (A) nella figura qui a destra,
potrebbe essere proprio una porzione dell'immagine. Se traduciamo
questa luminosità (punto dopo punto) in una curva, si ha la
curva B. La curva B assomiglia molto ad un segnale video che esce da una
videocamera. Questa curva ha un andamento "analogo" rispetto a quello
della luminosità che l'ha generata, perchè sale quando sale
la luminosità, scende quando scende la luminosità. E quindi
l'onda in B è un' onda "analogica". Inizia qui la conversione analogica/digitale.
LA CONVERSIONE
![]()
La conversione analogica/digitale avviene con un procedimento chiamato
"campionamento". Ad intervalli regolari, scanditi da un oscillatore (clock)
viene misurata la curva: nella figura della pagina precedente si vedono
in C sette frecce che cadono dall'alto in basso, e simboleggiano sette
misurazioni effettuate sulla base di una certa frequenza predeterminata,
su cui torneremo più tardi. La distanza della curva dallo zero -in
ciascun momento in cui cade la misurazione- può essere rappresentata
da un numero decimale. Ad esempio, 5,6,7,8,7...
Qui è importante notare una cosa. Occorre fare bene i
conti con il numero massimo di valori che può assumere ciascuna
misurazione. Se ciascun punto trasportasse 1.000.000 di possibilità
(ovvero, se ciascuna misurazione potesse assumere un numero tra 1 e 1.000.000),
si avrebbe una misurazione molto precisa, ma occorrerebbe trasportare una
massa di dati enorme. Ogni 500.000 misurazioni (quel tanto che basta
a trasportare una buona immagine video) servirebbero (500.000 x 1000.000=
500 miliardi di informazioni. Se invece vi sono solo 4 possibilità,
ecco che per ciascun punto basta trasportare 4 valori. Per 500.000
misurazioni, bastano due milioni di informazioni. Tra 2 milioni e 500 miliardi
c'è una bella differenza. Ma anche un'immagine di 4 toni è
ben differente come qualità rispetto ad una immagine con un maggior
numero di valori intermedi. Su questo rimandiamo a quanto detto a
suo tempo circa la "scala dei grigi", e alla figura con 2 valori, 4 valori
di grigio e 256 grigi.
In buona sostanza, il risultato della misurazione deve poter assumere
un numero di valori limitato, se si vuole avere una quantità
di dati ragionevole, ma deve assumere un numero di valori elevato se si
vuole avere una qualità d'immagine decente. Queste due esigenze
contrapposte non possono trovare risposta se non in una situazione di perenne
compromesso.
LA FREQUENZA DI
CAMPIONAMENTO
![]()
Oltre che al numero di valori che può assumere ciascuna misurazione,
passiamo a considerare il numero di misurazioni che servono. Anche
qui, la situazione è più o meno la stessa: un grande numero
di misurazioni comporta un'immagine più accurata, ma aumenta la
massa di dati da trasportare, da registrare, da manipolare. Abbiamo
già accennato nella puntata scorsa ad un problema di importanza
fondamentale: l'intervallo tra una misurazione e l'altra dev'essere abbastanza
stretto, altrimenti tra una misurazione e l'altra potrebbero esserci delle
variazioni significative del segnale che noi non cogliamo in quanto non
vengono misurate, cadendo appunto tra due misurazioni. Se tra la misura
2 e la 3 ci fosse un picco della curva, questo non verrebbe "visto", in
quanto si conserverebbero i dati del punto 2 e del punto 3, senza
quello intermedio. Con quanta frequenza dev'essere misurata una curva?
In altre parole, quanto deve distare nel tempo una misurazione dall'altra?
E' stato detto che la frequenza del campionamento (la frequenza delle
misurazioni, in cui viene fatto un "campione" della curva) segue la legge
di Shannon: occorre misurare con una frequenza almeno doppia rispetto
a quella della massima frequenza da conservare. Cosa consegue da ciò?
Che la frequenza di campionamento è in funzione della risoluzione
massima che vogliamo avere. Se vogliamo avere un grande numero di particolari,
di dettagli sullo schermo, ecco che avremo molte variazioni di luminosità
di piccole dimensioni (es., i fili dell'erba quando inquadriamo un pezzo
di prato) e quindi dovremo avere delle frequenze elevate e
di piccole dimensioni, e quindi una fitta serie di misurazioni, in numero
almeno doppio rispetto a quello della frequenza dell'onda da registrare.
Se ci accontentiamo di una frequenza più bassa, vedremo meno
variazioni di luminosità, e -se siamo davanti al prato di prima-
non si potranno più vedere i singoli fili d'erba, ma
si vedrà solo un cambiamento di tono più o meno uniforme.
Secondo l'espressione di Hartley, Tuller, Wiener e Shannon, la
quantità totale dei numeri binari (degli impulsi) da trasportare,
è legata sia al rapporto segnale/rumore che alla larghezza della
banda, ovvero al numero delle frequenze impegnate. Questo secondo aspetto
è abbastanza ovvio, sulla base di quanto fin qui detto: se per convertire
frequenze maggiori occorrono molte misurazioni in più, è
evidente che alla fine si avranno molti più numeri da gestire, numeri
che sono il frutto delle maggiori misurazioni. Sarebbe come dire
che se per misurare una tavolo si prendono dieci misure, si
hanno più numeri che se prendiamo solo due misure.
Il RAPPORTO SEGNALE/RUMORE
Anche l'aumento del rapporto segnale /rumore richiesto comporta un aumento di dati. Iniziamo con il rammentare che per "rumore" non si intende nulla di acustico, ma semplicemente si indica il disturbo di fondo che è presente sia nelle immagini che in qualunque altro segnale. Il rapporto segnale/rumore (indicato come S/N o S/R) indica la "distanza" tra il segnale utile e il disturbo di fondo. Maggiore è questa distanza, meno il segnale è inquinato da rumore, e quindi l'immagine acquista in pulizia. Quindi, un'immagine televisiva con un rapporto segnale/rumore di 43 dB è più pulita, più nitida di una con 42 dB. Il dB (decibel) è una misura di guadagno, indica nel nostro caso quanto il segnale video "sovrasta" il livello del disturbo di fondo. Osservate la tabella nelle pagine precedenti, titolata "alcuni esempi". Vedrete che se su una linea telefonica accettiamo un rapporto segnale/ rumore modesto (differenza tra segnale e rumore di soli 20 dB) ecco che -a parità di frequenza massima, o meglio di banda passante- si ha un trasferimento di dati che è il doppio rispetto a quello che si ottiene quando si è più esigenti, e si vuole un rapporto segnale/rumore più favorevole. (=una distanza tra segnale e rumore di 40 dB). Le cose divengono più gravi se si passa nel mondo dell'immagine. Se ci si accontenta di un'immagine con una certa granulosità di fondo (35 dB di S/R) a parità di definizione (=banda passante) basta un flusso di 40 Mbit/s. Se si vuole un'immagine più "pulita", passando a 40 dB, la quantità di dati necessaria sale a oltre 65 Mb/s. Quindi, per incrementare la pulizia di soli 5 dB, occorre aggiungere 26 milioni di informazioni al secondo, oltre un miliardo e mezzo di informazioni supplementari per ciascun minuto di programma. Voi ora comprendete perchè spesso i costruttori sacrificano molto sul versante del rapporto segnale/rumore, che viene tenuto in minor considerazione da parte degli utenti rispetto alla risoluzione. Molti utenti sarebbero disposti a sacrificarsi per dieci linee di risoluzione in più, mentre un dB di S/R in più o in meno fa meno effetto. Tenete conto che le registrazioni digitali DVC che sono state presentate nella seconda metà del 1995, hanno invece un segnale rumore di 54 dB, con un fattore molte volte superiore rispetto a quello del rapporto tipico di molti sistemi video in uso. Questo è bene, si sta prendendo coscienza dell' importanza di questo dato.
IL FLUSSO DI DATI
:
O DURATA
O QUALITA'
![]()
Come si vede, per registrare un' immagine digitale di qualità
ragionevole, e quindi con una risoluzione accettabile (=numero di misurazioni
adeguato) e un S/N decente, si sale verso valori di dati al secondo enormi.
Non ripeterò troppe volte una cosa, che tuttavia dev'essere ben
tenuta presente come un tormentone che non vi deve mai lasciare: si parla
sempre di quantità di dati al secondo, e non di quantità
di dati in assoluto. Questo vuol dire che un nastro o un disco
ha una capacità assoluta. Ad esempio, una cassetta può avere
una capacità di 1000 Megab. Ebbene, ci si può domandare:
quanto programma può contenere? Non si può rispondere semplicemente
in termini di tempo: ad esempio, due ore o quattro ore. Se lo si registra
con un trasferimento di 20 Megab/secondo, si satura in
50 secondi, meno di un minuto di programma. Se lo si registra con un programma
di qualità più bassa ( ovvero con minore risoluzione
e S/R, in modo che si abbia un trasferimento di 2 Mb/s) lo
si riempie con oltre otto minuti , dieci volte tanto. Così,
una quantità "X" di dati può essere ottimale
per una sola immagine di buona qualità; ma questa immagine
dev'essere ridotta di qualità se lo stesso ammontare totale
di dati deve venire usato per gestire più immagini anzichè
una sola.
Questo principio spiega parecchie cose. Ad esempio, perchè
diversi standard presentano al loro interno più opzioni. Il sistema
D-VHS (=digital VHS) ne prevede ad esempio tre. Una è caratterizzata
da un C (trasferimento di quantità di dati per secondo)
di 2 Mbit/s. Su una cassetta VHS ci staranno circa 32 Giga-byte.
Facendo i dovuti calcoli, su una VHS (E240) ci stanno addirittura
49 ore di programma! Ma si tratta di un programma con una qualità
modesta. Se si aumenta il C, e si sale ad un'immagine di qualità
migliore, si passa all'opzione HD, con un trasferimento di
28,2 Mb/secondo. A questo punto però su un nastro ci sta meno programma;
ovvero, ci stanno solo due ore e mezza di programma. Ma ci sta un'immagine
con una banda passante e un rapporto segnale/rumore molto, molto migliori.
Tanto migliori che molti utenti preferiranno far durare un nastro due ore
e mezza anzichè 49 ore.
Questi risultati non si sono avuti semplicemente inviando la massa
di dati al nastro VHS, ma grazie ad un espediente senza il quale
il D-VHS non avrebbe visto la luce.
LA COMPRESSIONE
![]()
Da tempo stiamo girando attorno ad un problema che non ci dà
pace: se si vuole avere un'immagine di qualità buona, dobbiamo
avere a disposizione un enorme numero di dati. Se vogliamo usare dei nastri,
dei dischi, dei canali televisivi o dei cavi ragionevoli, possiamo impiegare
solo immagini di qualità modesta. Come si fa a risolvere questo
dilemma?
Negli ultimi anni è sorta una possibilità insperata,
che sta rivoluzionando tutto il mondo dell'audio, del video, dell'informatica
e di molti altri settori più o meno collegati. Ed è in fondo
il motivo per cui la digitalizzazione sta prendendo sempre più piede,
e sta diventando la parola d'ordine in tutta l'elettronica. Senza questa
possibilità che andiamo a descrivere, in queste pagine non parleremmo
di digitale, perchè il digitale non sarebbe entrato seriamente nel
mondo della videoregistrazione e dell'immagine in movimento.
Questa tecnica che sta imponendo la digitalizzazione a tutti i livelli
è la compressione.
In pratica, non si trasferiscono i dati così come vengono letti
dall'immagine luminosa trasformata in digitale, ma vengono trasferiti (letti,
elaborati, registrati, inviati via cavo o via etere) impacchettati in forma
compressa.
Vi sono diverse tecniche di compressione, che possono essere classificate
in diverso modo. Ad esempio, in "lossy" e "non-lossy". Inoltre, queste
tecniche sono definite in certi standard, che prendono il nome dal gruppo
che le ha formate. Ad esempio, un insieme di tecniche è stato standardizzato
come MPEG, in quanto formato dalla commissione "Motion Picture Expert Group",
ovvero "Gruppo di esperti dell'immagine in movimento". E' una commissione
appartenente all'organizzazione internazionale "ISO". Ma prima di
entrare nei dettagli delle tecniche usate nei sistemi di videoregistrazione
digitale presenti oggi all'orizzonte, occorre tuttavia iniziare chiarendo
bene a tutti cosa si intende per "compressione", cosa che verrà
fatta nel prossimo capitolo dedicato all'immagine digitale
LA
DIGITALIZZAZIONE
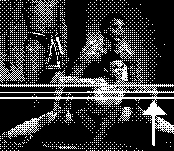 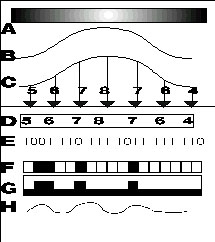 
Nella figura sopra, in corrispondenza delle freccia, c'è una variazione di luminosità. Proviamo a ingrandirla e rappresentarla in A nel disegno sotto. Essa corrisponde ad una curva analogica in B. In C, questa curva viene misurata a intervalli regolari (=campionata). La distanza tra il punto della curva e lo zero in ciascun istante è rappresentata da un numero. Si ottiene una fila di numeri decimali. Si consulta una tabella, e si attribuisce a ciascun numero decimale un numero binario (E). Questi numeri sono fatti di soli 0 e 1, e quindi si può ottenere una fila di impulsi digitali (es. bianco/nero, o acceso/spento), come in F. Questo codice è quello registrato su nastro (magnetizzazioni) o disco (le tacche dei CD) Notate che se si vuol rappresentare una curva analogica del codice binario (in H), si ha una frequenza maggiore di quella originale. |
|
| PER
SAPERNE DI PIU'
La
quantità di segnale che può essere trasmessa, elaborata o
memorizzata viene espressa in bit al secondo, ovvero "in quante informazioni
elementari" possono essere trasmesse in un secondo. E' qui simbolizzata
dalla lettera C. Essa è legata sia alla larghezza di banda (all'ampiezza
della gamma di frequenze che può essere trasmessa) sia al rapporto
segnale/rumore, ovvero alla possibilità di inviare i dati
con un disturbo più o meno marcato.
|
|
| ALCUNE
PRECISAZIONI
In
questo testo si fa riferimento esclusivamente alla luminosità dell'immagine,
ovvero all'immagine in bianco e nero. Ripetiamo che lo si fa per semplicità,
anche solo per non ripetere ogni volta che ciascuna misurazione può
avere un diverso valore di grigio e/o di colore. D'altra parte comprendere
la struttura e le operazioni sull'immagine in bianco e nero (formata da
un certo numero di grigi) può servire sia a comprendere come
funziona l'immagine a colori. Se qualcuno vuole riferirsi alla sola immagine
a colori, basta sostituire ai "i valori di luminosità" o "variazioni
di luminosità" le variazioni di tinta o i valori del colore x o
y. Cogliamo l'occasione per ricordare che un’immagine con 256 livelli
di grigio è un’immagine con un numero di sfumature ragionevole,
ed infatti costituisce un buono standard per le immagini in bianco e nero.
Ma non è sufficiente per avere una bella immagine a colori,
256 colori costituiscono un valore tollerabile ma non ottimale. Una
base di 8 bit (con tutte le possibili combinazioni) dà (8 elevato
2=) 255 valori. Quindi, occorre usare un sistema che legga più di
8 bit per misurazione. Perchè parliamo di "8"? Vi è un'unità
di misura nel mondo dei computer, che è il byte, formato appunto
da 8 bit. Quindi, un byte basta per un'immagine in bianco e nero, ma non
per una a colori, che può basarsi su sistemi a 16 , ma -ancor meglio-
a 24 o 32 bit. In effetti oggi i 24 o -più ancora- i 32 bit costituiscono
uno standard di fatto.
|
.
.
.
| L'IMPORTANZA
DELLA COMPRESSIONE
Tutte
le tecnologie paiono avere dei momenti di grande euforia, e poi delle fasi
di assestamento. E' facile notare che in pochi decenni si è passati
dagli aerei con le ali di tela ai Jumbo, e da qualche decennio ci si è
assestati con piccoli miglioramenti. Così, anche i televisori hanno
visto un loro enorme miglioramento in pochi anni, e poi si va avanti con
microscopiche innovazioni di cui magari l'utente non si accorge neppure
(parlo dei blak-matrix e compagnia bella). Anche la videoregistrazione
pareva arrivata in un momento di stasi: poche innovazioni e poco visibili
da parte del pubblico. Anche dei rinnovamenti profondi (il Super-VHS) hanno
inciso poco sul mercato perchè portano vantaggi scarsamente apprezzabili
da parte del pubblico. Ma eccoci ora ad una vera rivoluzione, che sta per
ridare un grande impulso a tutto il settore video, e che rimescola le carte
sul tavolo. Vi sono apparecchi amatoriali che superano di un balzo certe
prestazioni ottenute a fatica con macchine professionali, al punto che
certi standard professionali paiono destinati a scomparire entro breve
tempo. E' qui che si gioca il futuro di chi ha scelto di dedicarsi alla
ripresa: certe macchine e certi prodotti stanno per divenire obsoleti,
mentre si profila una rivoluzione di prestazioni e standard, tutta all'insegna
del digitale. Questa rivoluzione avviene grazie ad una tecnologia
che è esplosa negli ultimissimi anni: quella della compressione
dei segnali. Vi sono due assi su cui si vanno delineando tutte queste innovazioni:
lo standard MPEG e il JPEG. Tra i due, l'MPEG-2 è di certo il più
importante. Ma anche JPEG focalizza l'attenzione del
videomaker, perchè è in JPEG la registrazione digitale DVC,
proposta da case diverse e di prima grandezza come Panasonic, Sony, JVC.
Il MPEG è uno standard più efficiente, ma è in qualche
modo asimmetrico: la compressione è oggi difficile e costosa, mentre
la decompressione è abbastanza facile e economica. Attorno all'MPEG
si stanno aggregando le applicazioni in cui l'impacchettamento del segnale
(costosissimo) non è di pertinenza del privato. Ad esempio, è
in MPEG-2 la televisione digitale, che dovrebbe sostituire quella
attuale. E' in MPEG-2 il videodisco da 12" . In ambedue i casi, sia l'ente
radiotelevisivo che il produttore cinematografico possono permettersi un
compressore MPEG. E' invece in JPEG il sistema dedicato alle videocamere,
in quanto servirebbe mettere nella videocamera di costo contenuto
un compressore eccessivamente ingombrante e costoso. L' MPEG è poi
un sistema meno adatto al montaggio. Anticipo queste cose solo
per sottolineare l'importanza della compressione: il significato
di queste sigle e i dati tecnici che saranno visti più avanti.
|