L'IMMAGINE DIGITALE 
 
(SEGUITO- PAGINA 3/3)
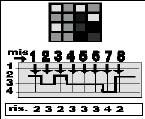
Qui  si si è ingrandito un particolare della figura 1B, quella con quattro livelli di grigio. Vedete che il primo quadretto è più chiaro, il secondo più scuro (la curva scende di un valore) , il terzo più chiaro ( la curva torna al valore del quadretto 1), il quarto torna al valore del 2, il quinto (nella riga sotto) resta allo stesso livello, così il sesto, al settimo si scende di un livello al di sotto del precedente, e quindi di due livelli al di sotto del quadretto 1... e così via. Misurando i singoli livelli di tutta la figura (e non solo di questo particolare ingrandito) , si ha alla fine una unica fila di gradini, ciascuno dei quali può assumere uno tra 4 valori, perchè l'immagine (come detto) è stata stampata con quattro differenti valori di grigio. Notate che la fila di gradini racchiude tutta l'immagine, perchè questa è stata letta in righe (leggendo i valori da sinistra a destra, e andando a capo per  iniziare a leggere la riga seguente.). Si deve ora osservare un fenomeno: se approssimiamo il nostro saliscendi dei gradini con un segnale, vediamo che la frequenza di questo segnale è variabile. Ricordo che la frequenza corrisponde al numero di variazioni al secondo: ebbene in corrispondenza delle misurazioni 4, 5, 6 ha una frequenza più bassa (perchè non vi sono variazioni per un certo intervallo di tempo) , mentre tra 1, 2 e 3 si registra una frequenza più elevata, in quanto vi sono più variazioni al secondo. Questo fenomeno ha delle implicazioni importanti, descritte nella figura seguente. Intanto, vediamo qui l'operazione di quantizzazione numerica, ossia di digitalizzazione vera e propria: si verifica il livello di ogni punto dell'immagine, e (in basso) si trae un valore discreto, un numero da 1 a 4 che codifica il livello di grigi. 

 

  
 
 
 
 
 
 
 
 
 
 
 		  
 
 
 
 
 
 
 
A                              B 
 
     A 1                       B1 

       C                         D 
 
      C1                       D1 
- 
- 
 

 nota 
 
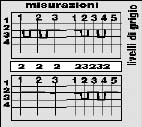
LA FREQUENZA DI CAMPIONAMENTO 
 
 
 

Immaginiamo di avere delle misurazioni ottenute come nella figura precedente. La curva A dà i valori : livello di grigio =2,2,2. Se dobbiamo ricostruire (sotto, in A1) l'immagine basandoci su questi dati, dobbiamo riprodurre solo lo stesso valore di grigio, cosa che non corrisponde all'immagine. Ed ecco il motivo per cui sotto vi sono i valori di 2,2,2...Cosa è successo? Che il numero di misurazioni al  secondo è troppo basso. Se raddoppiamo la frequenza delle misurazioni ( a destra, in B) ecco che il risultato delle misurazioni è 23232, e se ricostruiamo l'immagine con questi valori il risultato è corretto (vedi  il grafico in B1) 
Se però la frequenza dell'immagine è bassa, si trasportano informazioni inutilmente. Guardate la figura qui sotto: in C vedete una curva trasportata correttamente con 3 misure, in D non si fa che ripetere i numeri.  La legge di Shannon infatti lega il numero di misurazioni utili e necessarie alla  frequenza  del segnale (dell'immagine) . In altre parole, per rendere tutti i dettagli di un'immagine (o di un qualunque altro fenomeno da digitalizzare, come ad esempio un suono) occorre effettuare un numero di misurazioni minimo, sotto il quale le variazioni che si hanno tra una misurazione e l'altrta non possono essere colte. 
La legge si Shannon parla infatti di un numero di misurazioni almeno doppie rispetto alla massima frequenza contenuta nel programma. 
Un programma con 10 variazioni di luminosità al secondo avrà bisogno di 20 misurazioni al secondo, un programma con suono di 1000 Hz avrà bisogno di 2000 misurazioni al secondo. 
1-Ecco perchè nel compact disc si è adottata una frequenza di campionamento (=di misurazione) di c.a 44KHz (44.000 misure al secondo). Per poter registrare anche le massime frequenza udibili, che sono nell'ordine dei 20.000 Hz o meno. 
2-Nell'ambito video analogico la frequenza di campionamento sarà legata alla risoluzione o definizione che si vuole ottenere, ovvero al numero delle linee per pollice, proporzionali al numero dei dettagli per centimetro (vedi anche il box su LINEE E RISOLUZIONE). 
3-Anche nel video digitale la frequenza delle misurazioni è proprozionale alla risoluzione, e quindi al numero di pixel significativi che si vogliono dare all'immagine. 
 
 

 - 
- 
- 
- 
- 
- 
- 
- 
- 
- 
- 
- 
- 
- 
- 
 
 
torna all'indice