...
un doveroso approfondimento
|
struttura
e funzionamento
degli
altoparlanti e delle casse acustiche
|
||
| ...
... |
||
|
un doveroso approfondimento |
| ------------------------------ | riassunto della puntata
precedente
|
------------------------- |

Qui sopra vi è uno schema con la struttura semplificata di un altoparlante. In realtà la sua costruzione è un po' più complessa, ma qui vi sono le sua parti principali. Partendo da sinistra possiamo notare il magnete (una calamita permanente che ha il compito di creare il campo magnetico in cui si muove la bobina). 1-Il
magnete è saldato ad una struttura che è di lamiera stampata
in alcuni casi, e di metallo pressofuso in altri. Questa struttura viene
chiamato "cestello". Oltre a sorreggere il magnete, sorregge anche il cono.
|
------------------------ | Ecco qui sotto l' esempio di un altoparlante reale, ed anzi particolarmente complesso, di marca Pioneer. Si possono distinguere con facilità tutti gli elementi che compongono lo schema della pagina precedente: a destra c'è il magnete, a sinistra il cono, al centro la bobina... Oltre
a quegli elementi, qui si possono vedere anche altre parti come la sospensione
che tiene "centrata" la bobina e il cono rispetto al cestello e il bordo
del cestello che va fissato al supporto
|
| E' stato detto genericamente
che un altoparlante è un dispositivo elettromeccanico, ma è
arrivato il momento di approfondire questo concetto. Molti tecnici considerano
un altoparlante un dispositivo a due stadi: uno elettromeccanico e uno
meccanico-acustico. Infatti nell'altoparlante entra il segnale amplificato,
che agendo nella bobina immersa nel campo magnetico prodotto dalla calamita
genera uno spostamento meccanico. Lo spostamento meccanico della bobina
viene impresso al cono. Il cono a sua volta si sposta grazie al suo montaggio
su una sospensione elastica, e quindi sposta l'aria, che genera il suono.
Quindi l'abbinamento corrente-bobina traduce la corrente in uno spostamento
meccanico (per questo è detto stadio elettro-meccanico) e
l'accoppiamento tra la bobina e il cono produce una trasformazione del
movimento meccanico in suono, e per questo viene chiamato stadio meccanico-acustico.
Ciascuno di questi due stadi ha le proprie impedenze. Infatti la bobina
è caratterizzata dall'impedenza elettrica, così come è
stata descritta nei primi capitoli di questo corso. Il cono che viene mosso
da quella offre la sua impedenza, ed è un'impedenza meccanica, perchè
"resiste" agli spostamenti che gli vengono impressi in modo variabile a
seconda della frequenza di questi spostamenti . Infatti, è del tutto
immaginabile che resista in maniera diversa quando gli vengono impresse
ventimila spostamenti al secondo (20.000 Hz) rispetto a quando gli vengono
impressi 10 spostamenti al secondo. Questa "resistenza" (essendo opposta
ad una frequenza, alternata) è quindi una impedenza, ed una impedenza
che varia anch'essa al variare delle frequenza.
I progettisti di altoparlanti tengono conto dell'accoppiamento tra la impedenza elettrica e quella meccanica proprie di un altoparlante. Cosa fa sì che un cono "resista" alla sua messa in moto da parte della bobina? L'impedenza meccanica di un altoparlante è
data soprattutto:
|
||||||||
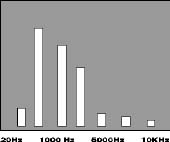 |
Memorizzando le varie frequenze che si incontrano nella musica, ed analizzando la potenza a cui vengono emesse, si possono costruire dei grafici chiamati "spettro sonoro". Le frequenza più basse (pur offrendo una potenza molto elevata) sono riscontrate nei programmi musicali più raramente rispetto alle frequenze medio-acute, che sono quelle maggiormente presenti. Questo aumenta il loro volume totale alla fine della memorizzazione. Se si analizza il suono alle varie frequenze senza memorizzarlo registrando semplicemente il volume a cui l'altoparlante emette le varie frequenze, si ha comunque una enorme prevalenza di volume sui bassi.
|
|||||||
| E' più
restio ad essere messo in moto un altoparlante con una massa molto grande,
ovvero di grandi dimensioni e pesante. L'altoparlante si muove più
facilmente se la sospensione (ci si rifaccia alla figura delle pagine precedenti)
è molto elastica, e non gli oppone resistenza. E' invece più
impedito nel suo moto se la sospensione è rigida.
Le sospensioni di alcuni altoparlanti (specie se economici) sono delle semplici ripiegature di cartone (il cartone del cono viene ripiegato a fisarmonica). Negli altoparlanti più evoluti e migliori la sospensione è costituita da un apposito materiale, molto elastico. Gli altoparlanti difficilmente sono mossi in aria libera. Sono di solito montati su uno schermo, e quando sono montati su una cassa chiusa di piccole dimensioni, anche l'aria "frena" il cono, opponendosi (quando il cono va indietro) a che l'aria di riduca di volume, (quando il cono va avanti) l'aria di decomprima. Ovviamente l'aria di comprime e si decomprime, ma l'inerzia dell'aria contenuta all'interno della cassa partecipa al sistema si sospensione del cono, acquistando un notevole valore nel gioco delle resistenze. Di per sè la potenza irradiata non è funzione della frequenza. A tensione costante. d un certo punto si può notare che la resistenza meccanica varia al variare della frequenza, e si ha una curva con una pendenza tipica di 6 dB per ottava. Ovvero, salendo in frequenza, per ogni ottava (ad esempio dal la2 del pianoforte al la3) si scende di 6 dB. Ricordiamo per inciso che il dB (=decibel) è un decimo di Bell, misura di guadagno. Un valore in deciBel negativo è dunque tipico di una perdita. Si dice che in un altoparlante si ha ha una condizione di controllo della massa con uscita costante sotto un punto (Kr) poi si ha una discesa con una pendenza di 6 dB per ottava Se si hanno condizioni di cedevolezza costanti (la cedevolezza è il contrario della resistenza meccanica di cui si è parlato) si ha una potenza che aumenta di 6 dB/ottava |
|||||||||||||
|
|
|||||||||||||
 |
 |
||||||||||||
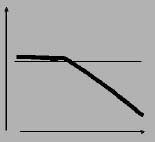
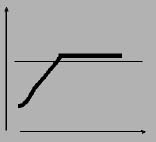
| il controllo di massa | il controllo di cedevolezza | ||||||||||||
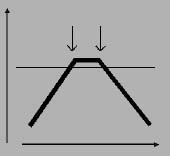
| la somma dei due effetti | ||||||||
 |
||||||||
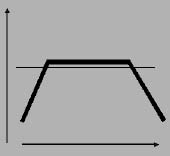
| Abbinando il controllo di massa (a destra) con il controllo di cedevolezza (a sinistra) e la relativa parte ad uscita lineare, ecco che si ha la risposta in frequenza dell'altoparlante. In questo caso è però poco estesa, nel senso che investe poche frequenze: questo altoparlante restituisce a piena potenza solo le frequenze comprese tra le due frecce che guardano in basso. | ||||||||
| la risposta in frequenza | ||||||||
 |
||||||||
| Abbassando la parte interessata dal controllo di cedevolezza verso frequenze più basse, e spostando la parte del controllo di massa verso le frequenze più elevate, ecco che la risposta in frequenza aumenta; ovvero, la parte della linea più elevata del grafico (qui il suono viene reso alla potenza più alta) va da frequenze più basse a frequenze più acute... | ||||||||
| fino ad un punto Kr.
Questo è un andamento detto "a velocità costante".
Da qui in poi la potenza irradiata non varia al variare della frequenza. Il fenomeno del controllo di cedevolezza comporta un aumento della potenza irradiata di 6 dB per ottava fino al punto Kr2, dopo il quale si ha un'uscita costante indipendente dalla frequenza. In un altoparlante ideale, si ha un controllo di cedevolezza a frequenza molto bassa, e un controllo di massa ad una frequenza molto alta: in questo modo, si ha un altoparlante con un' uscita lineare e quindi con una risposta in frequenza costante ed estesa (vedi figura in questa pagina, quella più sotto) La risposta in frequenza degli altoparlanti è forse il loro parametro più critico. La loro risposta nell'intero spettro acustico può essere divisa in cinque parti: nella prima parte (A) la potenza (a parità di segnale d'ingesso) aumenta di 12 dB per ottava, vi è poi una zona B dove per il controllo di cedevolezza aumenta di 6 dB per ottava, una zona ad irraggiamento acustico costante al variare della frequenza, poi una zona (D) in cui per effetto del controllo della massa si ha un decremento di 6 dB/ottava, e infine una zona con un decremento di 12 dB/ottava a causa della reattanza induttiva della bobina generata dall'aumentare della frequenza. Si noti che quanto previsto per la parte B corrisponde solo parzialmente all'andamento reale dell'altoparlante, perchè qui cade la frequenza di risonanza dell'altoparlante. Qui l'altoparlante sottosmorzato può incrementare la pressione sonora emessa, ma si tratta di una emissione distorta e non lineare, quindi da evitare. Si cerca allora di far cadere questa risonanza in una gamma di frequenza che si la più bassa possibile, per farla cadere in un'area dove il guadagno (= il livello in decibel) è minimo. La potenza d'uscita che viene qui considerata è quella posta sull'asse dell'altoparlante. In realtà se ci si sposta lateralmente questa potenza può diminuire in modo anche rilevante. La diminuzione si ha nella pratica solo alle frequenza elevate, perchè con le comuni dimensioni dei coni, la sorgente di suono è molto più piccola rispetto alle dimensioni delle onde, e quindi può essere considerata una sorgente puntiforme. La stessa cosa non può dirsi per le onde generate da un cono le sui dimensioni possono essere paragonate a quelle della frequenza generata. Immaginiamo di avere un altoparlante che emette una frequenza elevata, come nella figura nella pagina seguente. Se poniamo davanti un microfono e misuriamo la potenza captata, vediamo che questa potenza è massima in asse e diminuisce man mano si aumenta l'angolo in cui si posiziona il microfono. Naturalmente la misurazione va fatta tenendo uguale la distanza tra il microfono e l'altoparlante. |
||||||||
|
|
|||||||
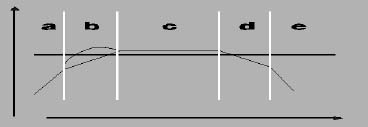 |
Qui
vi sono le cinque parti in cui può essere suddivisa
|
||||||
| NOTA
Il prossimo argomento verrà trattato anche in un altro articolo dedicato all'Hi-Fi e all'ambiente. L'interesse per questo fenomeno riguarda infatti sia il comportamento ell'altoparlante da inserire in una cassa (in questa sede) he gli effetti tipici di una cassa che suona in un ambiente. |
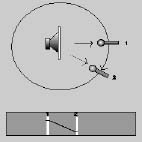
Vediamo come si comportano gli altoparlanti rispetto all'angolo di ascolto.
Immaginiamo di avere un altoparlante che emette una certa nota (esempio, 440 Hz) a volume costante. Immaginiamo anche di porre un microfono davanti ad un altoparlante, e di misurare il livello sonoro (1) riportandolo sotto. Spostiamo ora il microfono di un certo angolo, mantenendolo però alla stessa distanza dall'altoparlante, ed effettuiamo una seconda misurazione (2).
Si può verificare che il volume del suono (nel punto in cui è in 2 nella figura) è più basso.
Procedendo in modo analogo, è possibile misurare con continuità il volume del suono facendo fare al microfono un giro completo, da 0 a 360 gradi. E' possibile ottenere un risultato come nella curva B: si vede che il volume del suono è massimo davanti al microfono (zero gradi) scende man mano si va verso i lati (90 gradi) aumenta un po' dietro (perchè riceve il suono prodotto dalla parte posteriore del cono) e poi torna ad abbassarsi (270 gradi) fino a tornare alto al punto di partenza (360 gradi).
In realtà non si usa costruire una curva come quella descritta sopra. In genere si preferisce costruire un "diagramma polare". In pratica, le variazioni di livello di scrivono su un foglio di carta circolare, come nella figura accanto. Quando il suono cresce in volume, il pennino che disegna la curva va verso l'esterno. Quando il suono cala di volume, il pennino torna verso il centro del cerchio. E' facile immaginare dove si trovava il microfono quando il pennino ha disegnato la curva in ciascun punto: man mano il microfono gira attorno all'altoparlante, anche il pennino si trova a quel preciso angolo.
Si ottiene così un diagramma che ha un significato abbastanza intuitivo: la linea comprende un'area maggiore là dove il suono ha una forza maggiore. Si può anche studiare facilmente l'andamento del volume, e si possono confrontare con molta facilità gli andamenti dei vari altoparlanti.
Nella figura C si può vedere infatti un altoparlante che (come da copione) ha un volume molto alto davanti, emette un suono più debole man mano vi va verso i lati, eccetera. Anche in D si ha un altoparlante per il quale possono essere dette esattamente le stesse parole; ma i volumi ai vari angoli sono differenti. In particolare l'altoparlante sotto ha una diffusione angolare più ridotta.
All'inizio
di questo discorso abbiamo dato per ipotesi che l'altoparlante emette una
certa nota. E' importante notare che queste due curve potrebbero essere
dello stesso altoparlante quando emette due diverse frequenze (ad esempio,
se emette 200 Hz si registra la prima, se emette 1000 Hz si registra la
seconda). Voi comprendete bene che questo fenomeno complica molto le cose,
se si vuole calcolare quanto volume sonoro produce un altoparlante, perchè
il volume totale nella stanza cambia con il succedersi delle diverse frequenze
contenute nella musica....
.
.
.
.
![]()
.
.
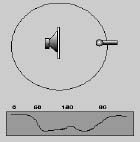
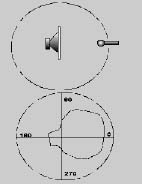

figura d